AHP Trees

An AHP Tree, or Simple AHP Hierarchy is a tree of criteria, with alternatives at the bottom. An example looks like:

In pyanp we work on such structures with the pyanp.ahptree module.

AHP Tree usage in pyanp

In this tutorial we will:

1. Show you how to import the AHPTree class (which is what handles all AHP tree calculations)
2. Read in a full AHP tree’s data from a single excel spreadsheet
3. Show some standard calculations and their results
4. Resources for this tutorial

1. Importing the AHPTree class

And a few other classes you will need for later parts of this tutorial

# Pandas has DataFrames and Series, very useful things
import pandas as pd
# numpy has lots of useful things in it
import numpy as np
# lastly import our ahptree python code.  If you haven't already installed the pyanp library do
# pip install pyanp
# to get it
from pyanp import ahptree

2. Loading data from an excel file

excel_file = 'PATH_TO_YOUR_EXCEL_FILE'
ahp = ahptree.ahptree_fromdf(excel_file)

3. Some standard AHP calculations

3.1 The global priorities for all users and the overall

gs = ahp.global_priority_table()
gs

	Group	Bill	John	Joseph	Ronald	Leanne	Blythe
Goal	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000
A	0.241823	0.191670	0.357156	0.167712	0.064374	0.073360	0.714286
A1	0.061971	0.011303	0.142862	0.041904	0.008701	0.008887	0.405327
A2	0.078277	0.037579	0.142862	0.015989	0.032055	0.058384	0.053618
A3	0.101575	0.142788	0.071431	0.109819	0.023618	0.006088	0.255340
B	0.321400	0.054852	0.234003	0.235756	0.679480	0.726685	0.142857
B1	0.154726	0.009142	0.033429	0.039293	0.509610	0.645942	0.114286
B2	0.166674	0.045710	0.200574	0.196463	0.169870	0.080743	0.028571
C	0.436777	0.753478	0.408841	0.596533	0.256146	0.199955	0.142857
C1	0.116491	0.251159	0.045427	0.074567	0.224128	0.019996	0.035714
C2	0.320286	0.502318	0.363414	0.521966	0.032018	0.179960	0.107143

3.2 Let’s graph the global priorities

gs = ahp.global_priority_table()
gs.plot(kind="bar")

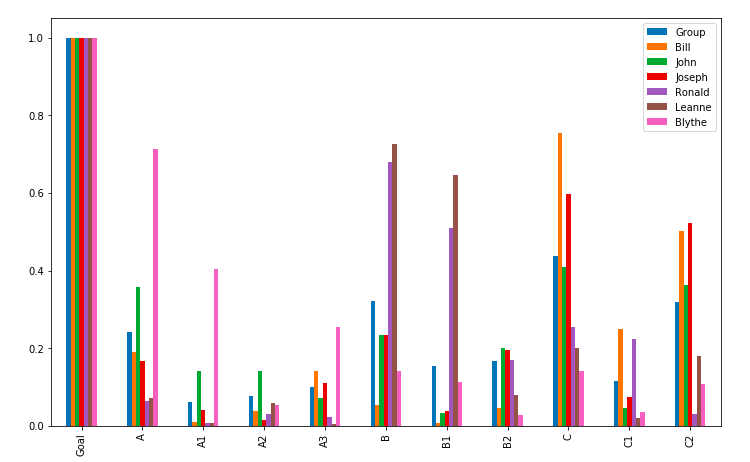
3.3 Now let’s get the synthesized alternative scores

altscores = ahp.priority_table()
altscores

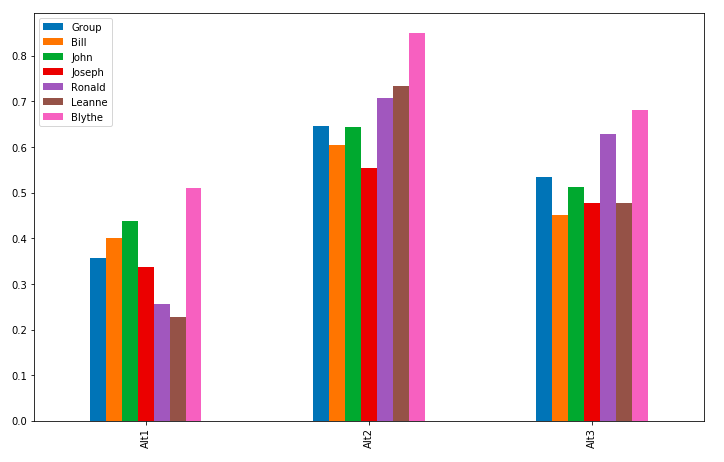
	Group	Bill	John	Joseph	Ronald	Leanne	Blythe
Alt1	0.356952	0.400781	0.438441	0.337148	0.256614	0.226740	0.509450
Alt2	0.645187	0.604409	0.644722	0.554433	0.707354	0.733468	0.851045
Alt3	0.533711	0.450100	0.512404	0.477552	0.629131	0.476311	0.681823

3.4 Let’s graph the synthesized alternative scores

altscores = ahp.priority_table()
altscores.plot(kind="bar")

3.5 Inconsistencies for all users and the group

allincons = ahp.incond_std_table()
allincons

	Group	Bill	John	Joseph	Ronald	Leanne	Blythe
Goal	0.056856	6.982872e-01	2.689665	1.767344e+00	0.164491	0.008849	-8.540177e-16
A	0.239585	5.580869e-01	0.480769	7.068608e-02	0.090399	0.096090	4.028993e-01
B	0.000000	4.440892e-16	0.000000	4.440892e-16	0.000000	0.000000	0.000000e+00
C	0.000000	0.000000e+00	0.000000	0.000000e+00	0.000000	0.000000	0.000000e+00

4. Resources for this tutorial

• Jupyter Notebook for this tutorial
• Excel file used